While in graduate school my advisor (Robert Joynt) asked me a question inspired by Mark Saffman’s work on neutral atom arrays. Generally, readout of neutral atoms scatters many photons, which can perturb the neighboring atoms. At that time, the neutral atom community had not yet figured out how to do mid-circuit measurement, posing a significant challenge for quantum error correction. However, qubit reset scattered significantly fewer photons. At the same time, neutral atoms offered the ability (using the Rydberg interaction) of performing native Toffoli gates and their higher-qubit generalizations. Thus, I was asked to explore the prospect of quantum error correction without measurement, but using qubit reset and multi-qubit gates.

The result (paper here) explores this task using the Steane code, and several novel techniques. First, we perform syndrome extraction using bare ancillas but using an overcomplete stabilizer set instead of just the stabilizer generators.

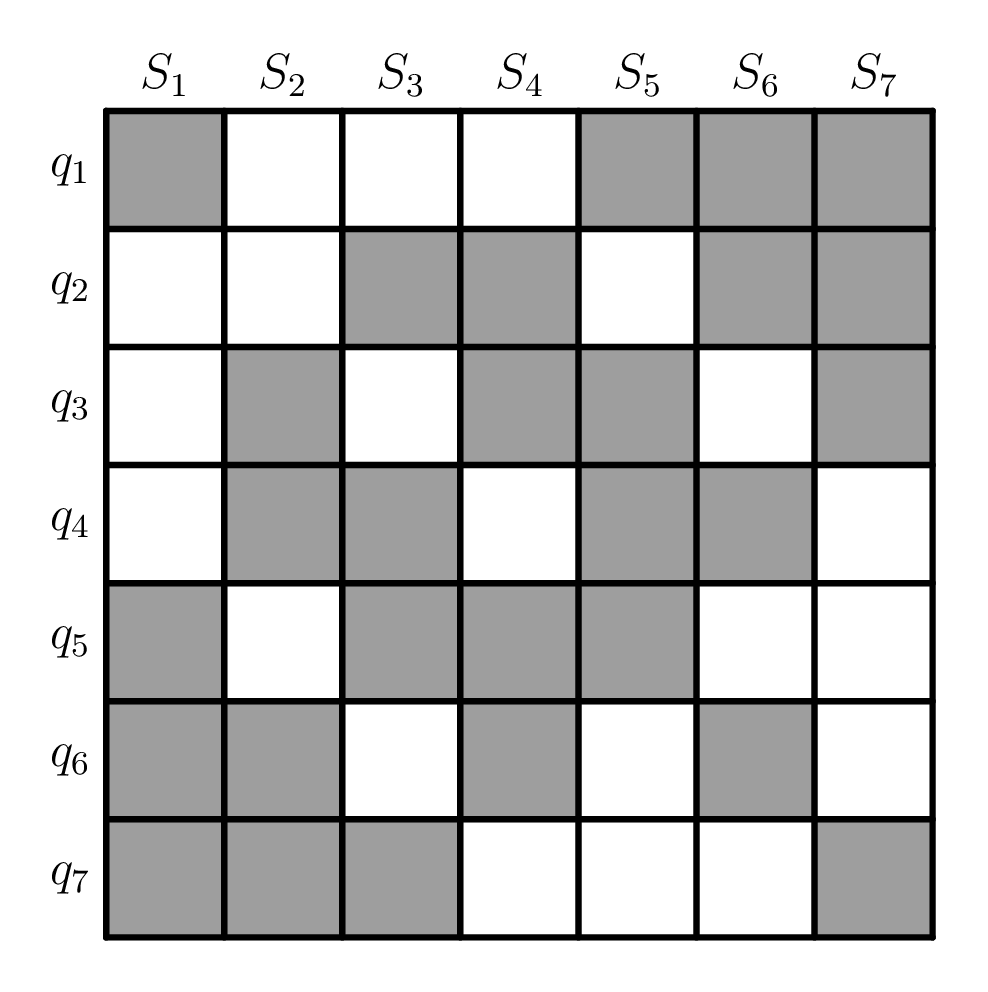
Overcomplete stabilizers of the Steane code

For the Steane code, the structure of all $Z$-type stabilizers is shown below, and can be generated by taking all non-trivial products of the standard $Z$-type stabilizers.

This structure depicts a combinatorial block design. (Confusingly, this example is a 2-design, but I avoid this terminology due to its other usage in the quantum information community.) It is easily seen from the diagram above that each qubit participates in 4 parity checks, and that any two qubits jointly participate in two stabilizer checks. To put it another way, 2 readout errors are required to confuse one syndrome with another. Thus, the full 7-bit syndrome can distinguish errors on the data qubits, even in the presence of readout error.

Decoding on quantum hardware

Decoding requires clasical logic. Given the 7-bit syndrome, errors on data can be corrected using generalized Toffoli gates with 4 control qubits, and iterating over all possible syndromes to correct each possible single-qubit error on the data.

A note on scalability

This work was initially focused on performing early error correction demonstrations using neutral atoms, although we explored further in subsequent papers.

It is worth emphasizing the difficulties in scaling this approach. Solving the decoding problem on quantum hardware is a daunting task. In the case of the Steane code, implementing a lookup-table decoder using generalized Toffoli gates is straightforward, at least theoretically. (Practically, it’s worth pointing out that despite much progress in Rydberg-based operations, native 5-qubit gates remain—to my knowledge—purely hypothetical.) For larger codes, implementing a full decoding algorithm is completely impractical. In principle, the approach could be used with concatenated codes and using hard decoding, but again—the prospect is daunting. That said, there is still some interest in the community about the prospect of measurement-free error correction. See this paper and this paper.

On the other hand, there has since been some encouraging work using overcomplete sets of parity checks (with measurement). For later work on overcomplete stabilizers, see this work from Earl Campbell and this work from Delfosse, Reichardt, and Svore.