Atom loss and 2-qubit gates

Atoms trapped in optical lattices have finite vacuum lifetimes. Furthermore, depending on atomic species and 2-qubit gate design, atom loss is a significant contributor to 2-qubit gate errors. Thus, atom loss presents a challenge for fault-tolerant quantum computing with neutral atoms.

Although other proposals exist, neutral atoms typically implement 2-qubit gates using the Rydberg interaction. While ground-state neutral atoms typically do not interact strongly, strong interactions can be induced by exciting neighboring atoms to states with large principle quantum number. This interaction can be used to implement a CZ gate by attempting to simultaneously excite both $\vert 1 \rangle $ states to the Rydberg state. The sequence is carefully calibrated so that if one or both atoms begin in the $ \vert 0 \rangle $ state, no excitation to the Rydberg state occurs and no overall phase is acquired.

If no excitation to the Rydberg level occurs for one atom, then there is no effect on its gate partner. If an atom is lost, there is no excitation to the Rydberg level. Thus, the effect on the gate partner of a lost atom is effectively an Identity gate.

Syndrome extraction with atom loss

Atom loss can only be detected between syndrome extraction cycles (using a knock-knock style protocol, or by swapping to data onto a different set of atoms). Syndrome information extracted is unreliable—if obtained at all—when qubits are lost during syndrome extraction. Unlike a typical erasure error, in which the precise temporal location of the error is known, atom loss is checked only between cycles, meaning that an entire cycle’s worth of syndrome information involving lost qubits is unreliable. Fortunately, due to the effective Identity gates on the partners of lost atoms, the effect of atom loss remains localized to a small spacetime region. These detected losses can be used to update decoding graphs.

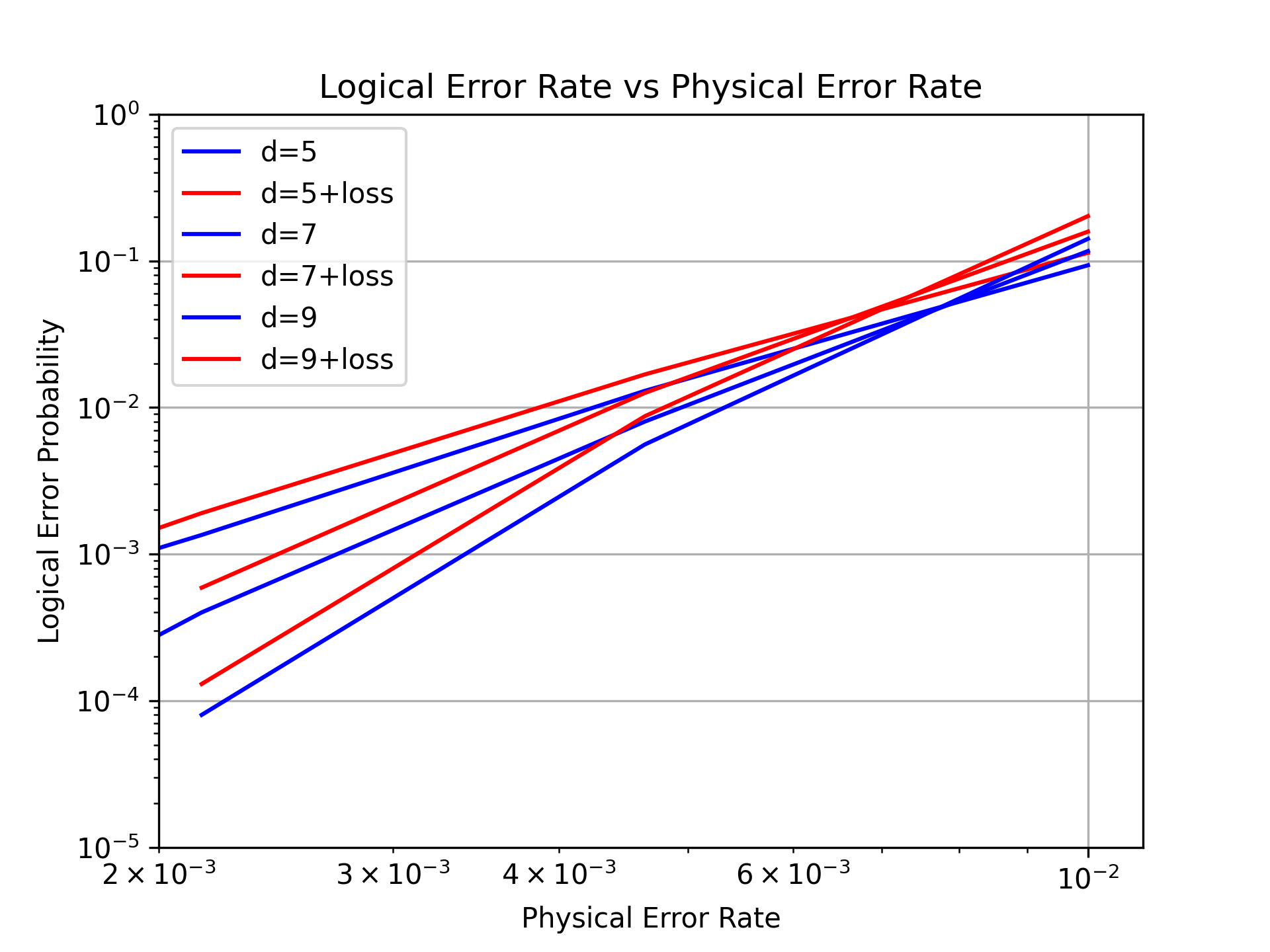
Simulations

To study the effect of atom loss on QEC, I performed simulations of surface code memory experiments in the presence of atom loss. The stabilizer computations were performed using Stim and decoding was performed using PyMatching. The results below use a standard depolarizing error model on 1Q and 2Q gates, SPAM error, and per-round idle error. All error mechanisms occur with equal probability. For simulations with loss, atom loss occurs per circuit timestep with the same probability. In the plot below notice the minimal effect of atom loss on threshold, and the parallel slopes for corresponding lossy and lossless curves.